FI – Fysiikka, aineisto

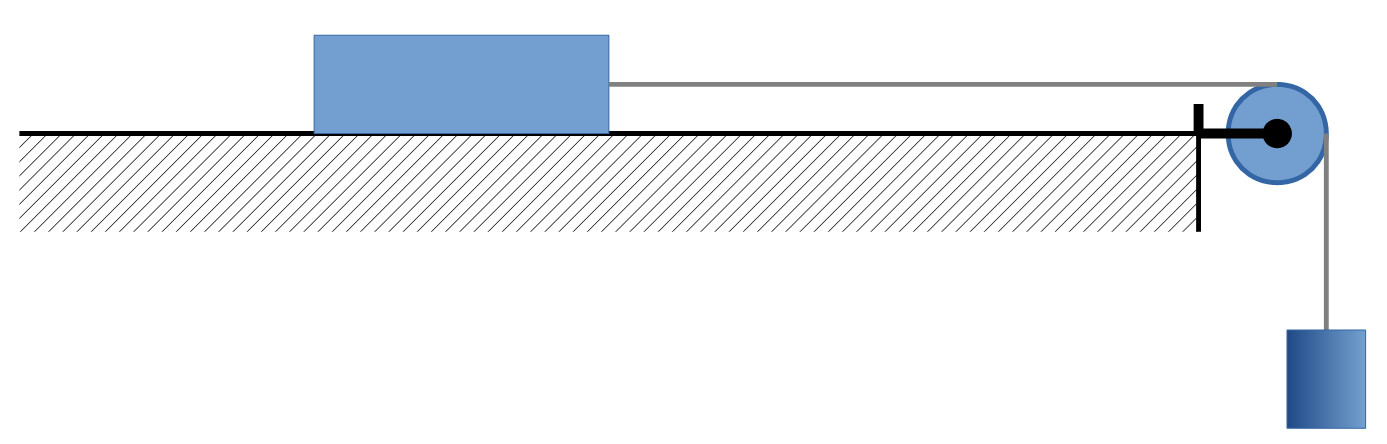
2. A  Kuva: Simulaatiossa mallinnettava järjestely

2. B Simulaatio: Laatikon kulkema matka ja nopeus ajan funktiona

Simulaatio avautuu napsauttamalla simulaation linkkiä. Muuta simulaatiossa laatikon massaa m_a ja punnuksen massaa m_b kaksoisnapsauttamalla vastaavaa taulukon solua ja syöttämällä uusi massan arvo (paina Enter). Simulaatiossa näkyvät taulukkona laatikon liukuma matka s ja nopeus v ajan t funktiona.

3. A  Taulukko: Tehtävässä tarvittavien suureiden keskimääräisiä arvoja

4. A  Kuva: Koejärjestely

4. B  Kuva: Valokuvio

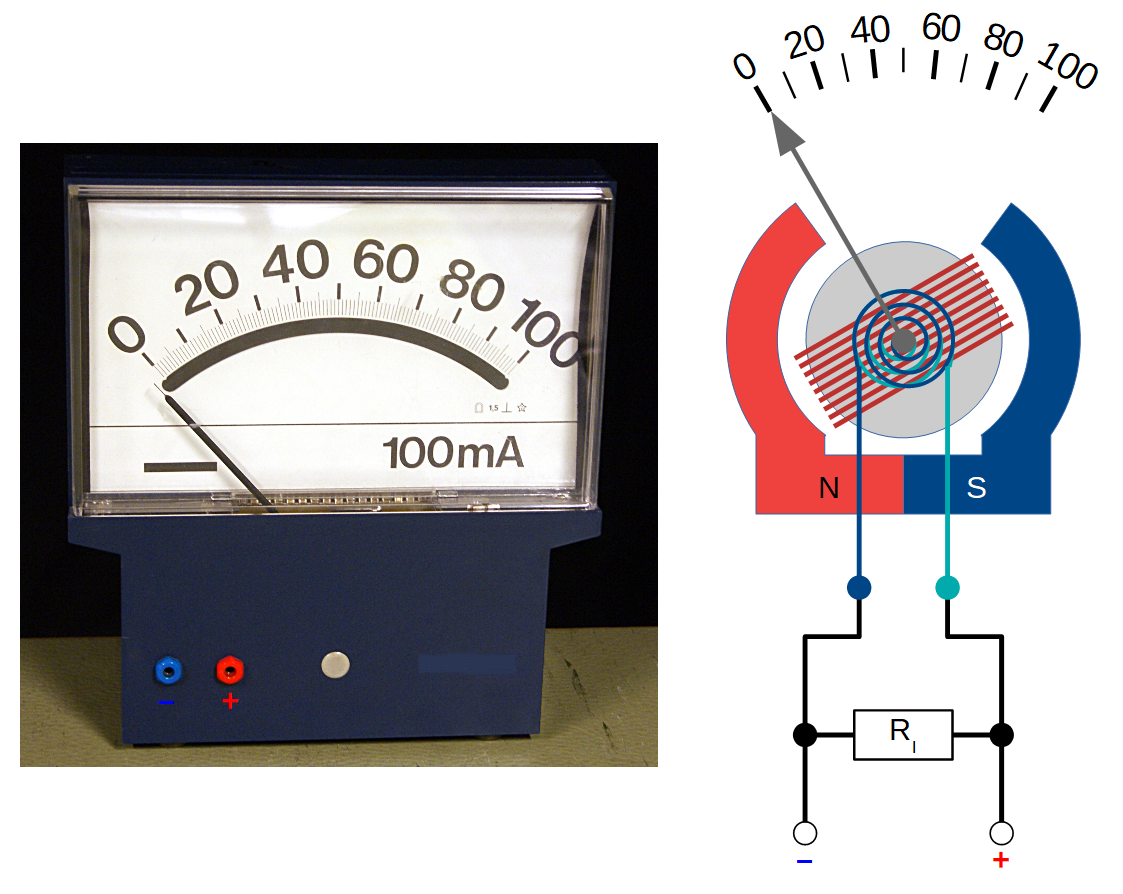
5. A  Kuva: Kiertokäämimittari ja sen kytkentä sähkövirran mittauksessa

5. B  Kuva: Kiertokäämimittari ja sen kytkentä jännitteen mittauksessa

6. A  Teksti: Helsingin Sanomien uutinen hypystä

Laskuvarjotta verkkoon 7 600 metristä

Laskuvarjohyppääjä Luke Aikins hyppäsi heinäkuun lopulla alle kahden minuutin vapaan pudotuksen ilman laskuvarjoa. Matkaa verkkoon oli 7 620 metriä. Aikins mätkähti 30 x 30 -metriseen verkkoon, joka oli viritetty Simi-laaksoon Kaliforniaan. Nopeutta oli lopussa hieman yli 190 kilometriä tunnissa.

Aikinsin kypärässä oli satelliittipaikannus, joka ohjasi häntä kohti verkkoa. Verkon valot muuttuivat punaisiksi, jos hyppääjä ajautui väärään suuntaan, kertoo Scientific American -lehti.

Aikins saattoi hieman ohjailla kulkuaan kahden minuutin pudotuksen aikana esimerkiksi laittamalla kädet pitkin vartaloa. Juuri ennen alastuloa hän kääntyi lennossa selälleen niin, että hänen selkänsä iski ensin verkkoon. Se toi joustoa iskuun.

Vapaassa pudotuksessa syntyy paljon liike-energiaa. Jos osuu maahan, kineettinen energia heijastuu maasta takaisin kehoon ja murskaa sen. Aikinsin pyydystänyt verkko oli valmistettu joustavasta polyeteenistä. Sen tiheä kudelma venyi sopivasti ja imi syöksyjän liike-energian. Verkon nurkissa oli neljä ilmanpaineella toimivaa sylinteriä, jotka niiasivat Aikinsin osuessa verkkoon.

6. B  Mittausaineisto: Hyppääjän korkeus ajan funktiona

Jokainen alla oleva tiedosto sisältää samat mittaustulokset. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

T6_B.ods (LibreOffice Calc)

T6_B.cmbl (Logger Pro)

T6_B.ggb (GeoGebra)

T6_B.vcp (Casio ClassPad Manager)

T6_B.tns (TI-Nspire)

7. A  Kuva: Sauvamagneetti pudotetaan käämin läpi

7. B  Mittausaineisto: Käämin sähkövirta ajan funktiona

Jokainen alla oleva tiedosto sisältää samat mittaustulokset. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

T7_B_fi.ods (LibreOffice Calc)

T7_B_fi.cmbl (Logger Pro)

T7_B_fi.ggb (GeoGebra)

T7_B_fi.vcp (Casio ClassPad Manager)

T7_B_fi.tns (TI-Nspire)

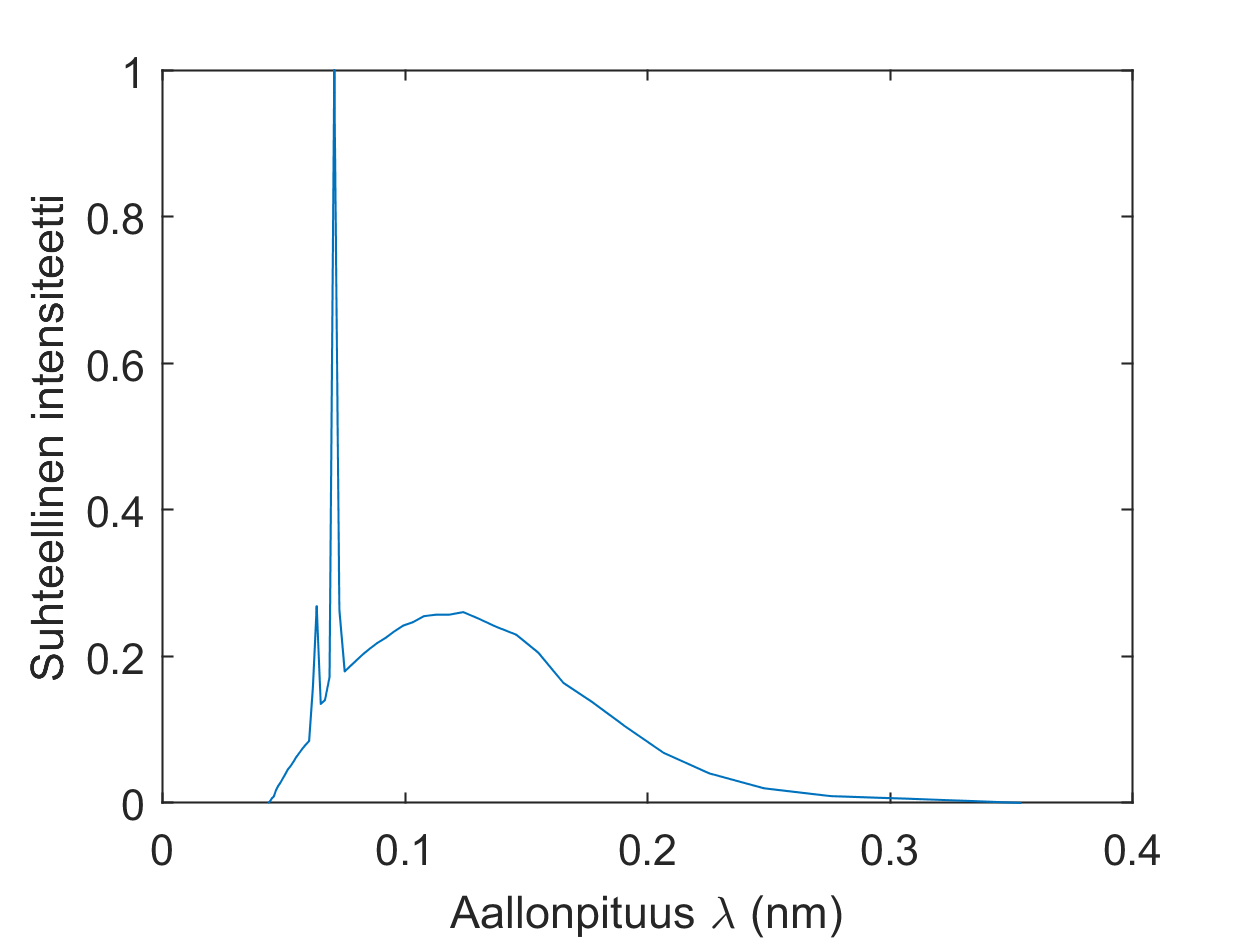
8. A  Kuva: Röntgenputken säteilyn spektri

10. A  Teksti: Painovoima-aallot ja LIGO

Advanced Laser Interferometer Gravitational Wave Observatory (LIGO) -koelaitteistossa Yhdysvalloissa saatiin ensimmäinen suora havainto painovoima-aalloista, GW150914, syyskuun 14. päivä vuonna 2015. Havainto vahvisti Einsteinin yleisen suhteellisuusteorian mukaisen ennusteen painovoima-aaltojen eli avaruusajan värähtelyjen olemassaolosta ja ominaisuuksista. Rainer Weiss, Barry C. Barish ja Kip S. Thorne saivat tästä havainnosta vuoden 2017 Nobelin fysiikan palkinnon.

Aiemmin painovoima-aalloista oli saatu vain epäsuoria todisteita, kun vuonna 1974 fyysikot Russell Alan Hulse ja Joseph Hooton Taylor Jr. havaitsivat kaksoispulsarin lähettämän sähkömagneettisen säteilyn vaihtelusta systeemin menettävän energiaansa täsmälleen saman verran kuin suhteellisuusteorian mukaan tällaisten toisiaan kiertävien neutronitähtien pitäisi lähettää painovoima-aaltoja. Hulsen ja Taylorin tutkimus palkittiin Nobelin fysiikan palkinnolla vuonna 1993.

LIGO-koelaitteiston äärimmäisen herkkä koejärjestely perustuu laservalon interferenssiä hyödyntävään mittausmenetelmään. Koelaitteistossa ohikulkeva painovoima-aalto venyttää kahta lasersädettä eri tavalla. Kun säteet yhdistetään, niiden vaihe-ero havaitaan interferenssinä, jonka perusteella saadaan painovoima-aallon aiheuttama suhteellinen venymä määritettyä.

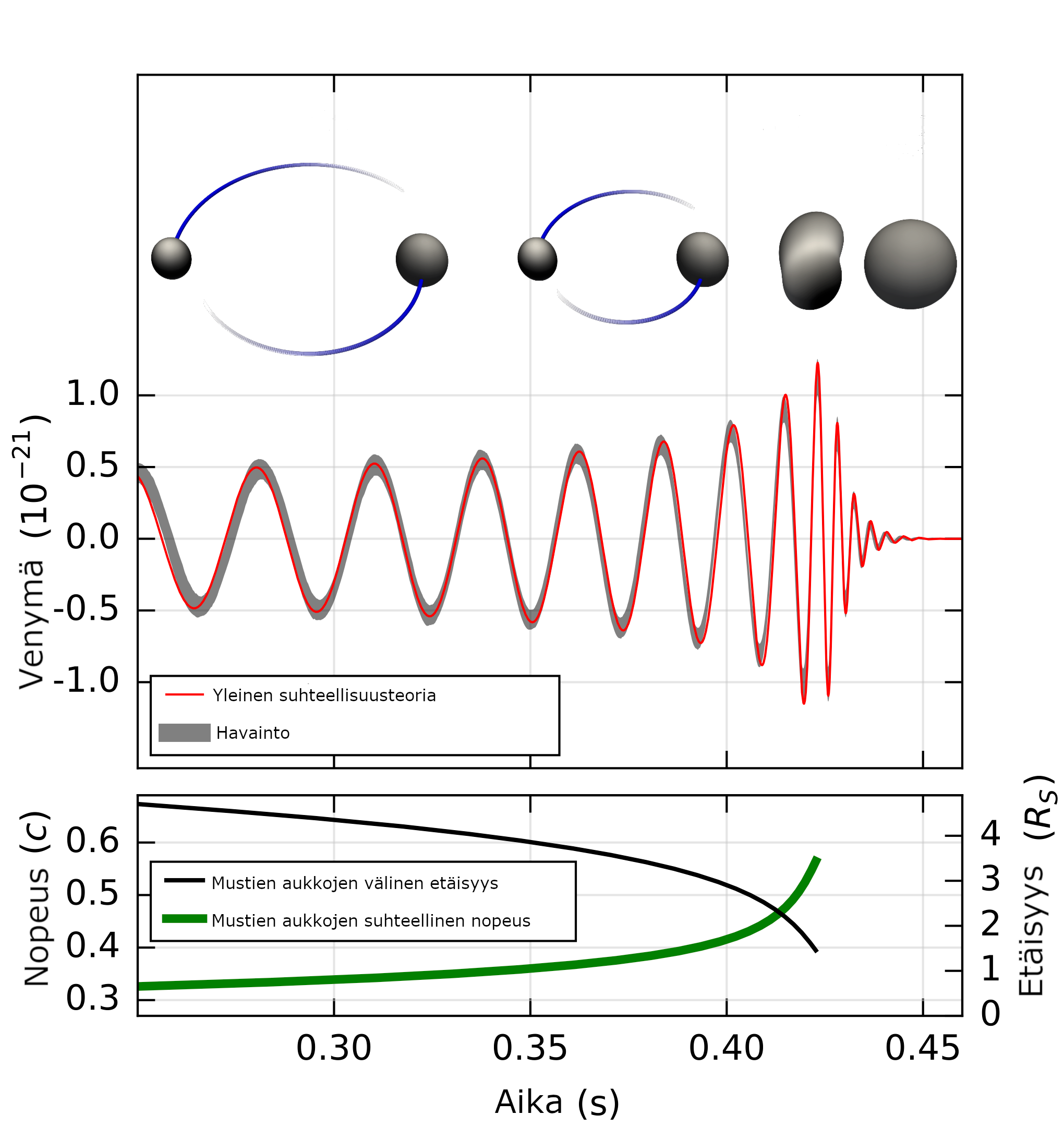
Kuvan 10. B ylemmässä paneelissa on esitetty havaintoon GW150914 liittyvä suhteellinen venymä ja sen yhteys kahden kappaleen liikkeeseen näiden yhdistyessä. Alemmassa paneelissa on ilmoitettu kappaleiden suhteellinen nopeus ja kappaleiden välinen etäisyys ajan funktiona. Etäisyys on annettu yhdistymisessä syntyvän kappaleen ns. Schwarzschildin säteen monikertoina. Schwarzschildin säteellä mitataan mustien aukkojen kokoa: Esimerkiksi kappaleen, jonka massa on 62 Auringon massaa, Schwarzschildin säde on noin 180 km.

Painovoima-aallot syntyvät kappaleiden kiihtyvässä liikkeessä. Havainnossa nähdään aluksi suhteellisen venymän oskilloiva osuus. Tämä voidaan tulkita ainoastaan kahden toisiaan kiertävän massiivisen kappaleen aiheuttamaksi. Taajuuden kasvu kertoo siitä, että kappaleet kiertäessään lähestyvät toisiaan. Signaalin taajuus kasvaa voimakkaasti, ja sen amplitudi pienenee nopeasti nollaan. Tämä kertoo, että kiertoliike lakkaa, kun kappaleet törmäävät ja sulautuvat yhdeksi.

Mittausdatasta saadaan määritettyä toisiaan kiertävien kappaleiden välinen etäisyys (ks. kuva 10. B), jota voi suhteuttaa tunnettujen taivaankappaleiden kokoon: tyypillisten tähtien halkaisijat ovat 100 000 – 1 000 000 km. Valkoisten kääpiöiden koko on yleensä kymmeniä tuhansia kilometrejä. Neutronitähdet ovat kooltaan pienimpiä, ja niiden halkaisija on 10–20 kilometriä. Neutronitähtien massa voi olla korkeintaan muutaman Auringon massan suuruusluokkaa.

10. B  Kuva: GW150914:n havaintodata

Kuvan ylempi paneeli näyttää havaitun venymän ajan funktiona ja toisiaan kiertävien ja yhteen sulautuvien kappaleiden rataliikkeen eri vaiheet. Kuvan alemmassa paneelissa on esitetty toisiaan kiertävien kappaleiden välinen etäisyys ja nopeus ajan funktiona. Etäisyys on annettu yksikössä R_S Schwarzschildin säde, joka on yhteensulautumisessa syntyvän kappaleen koko.

11. A  Kuva: Höyrypuhdistin

11. B  Kuva: Laitteen arvokilpi

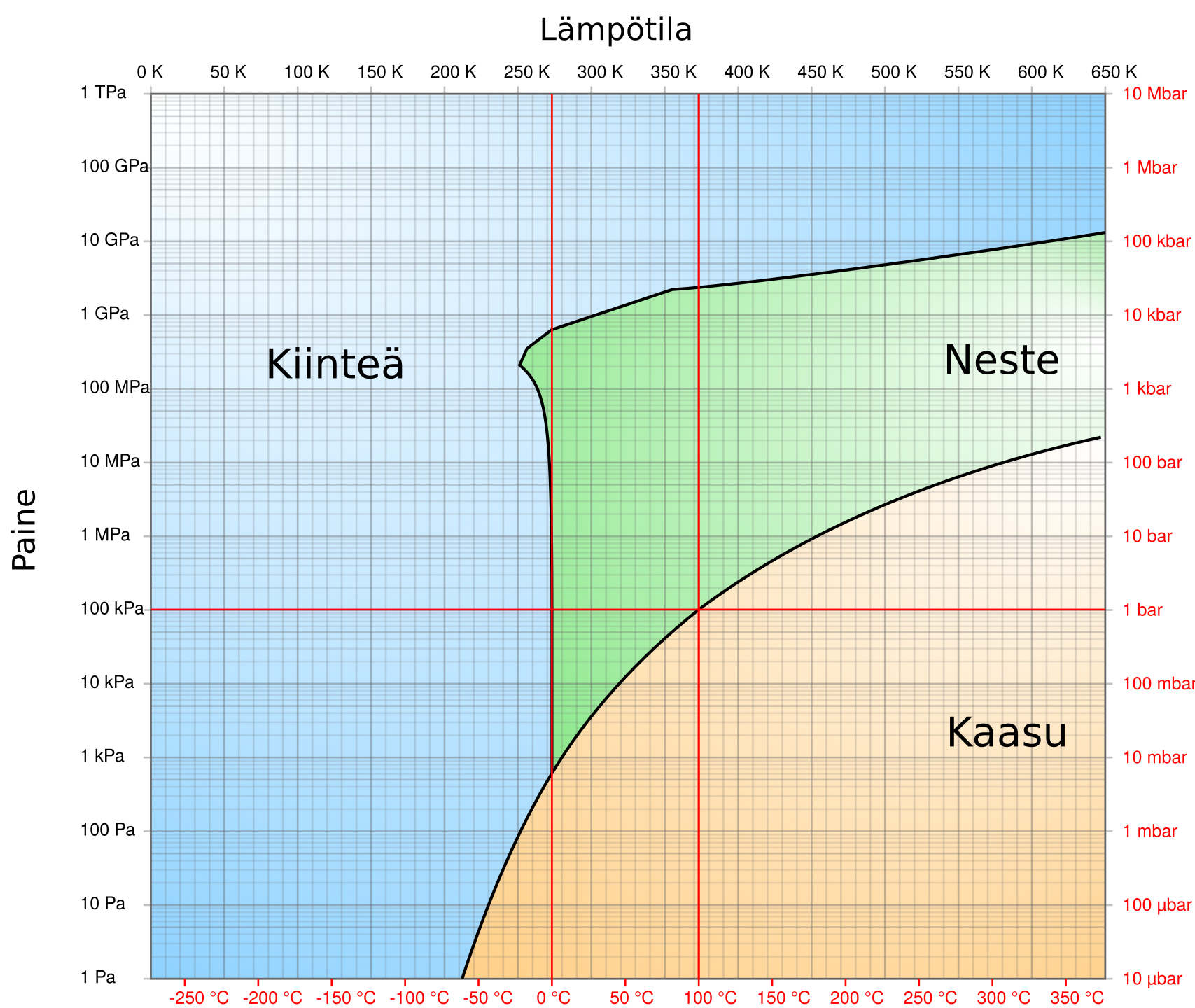
11. C  Kuva: Veden faasidiagrammi

Huomaa, että faasidiagrammin paineakseli on logaritminen.